лицензионное программное обеспечение
8 (495) 8 (812) 8 (800) |
|||||||||||
|
STATISTICA Advanced
Нужна подробная консультация по лицензированию и покупке? Обращайтесь!
Вы можете сделать заказ в свободной форме - заполните форму. Купить STATISTICA Advanced STATISTICA Advanced предоставляет углубленные методы анализа данных, включает все возможности продукта STATISTICA Base, а также следующие модули: STATISTICA Advanced Linear/Nonlinear Models (Углубленные линейные/нелинейные модели)
STATISTICA Multivariate Exploratory Techniques (Многомерные технологии анализа данных)
STATISTICA Power Analysis and Interval Estimation (Анализ мощности и интервальное оценивание)
STATISTICA Advanced Linear/Nonlinear Models (Углубленные линейные/нелинейные модели)STATISTICA Advanced Linear/Non-Linear Models предлагает широкий спектр линейных и нелинейных средств моделирования, поддерживает прогнозирование как непрерывной, так и категориальной переменной, взаимодействия, иерархические модели, возможность автоматического выбора моделей, а также компоненты дисперсии, временные ряды и другие методы. Все анализы снабжены разнообразными интерактивными графиками и встроенным редактором Visual Basic. Модуль предоставляет следующие возможности:
Подгонка и моделирование
Например, вы производите продукт и выделяете 3 важные качественные характеристики. Предполагаем, что если сумма первых двух качественных характеристик больше, чем удвоенная величина третьей характеристики, то продукт считается дефектным. Вместо того, чтобы ждать когда появятся требуемые данные, можно подогнать теоретические распределения к наблюдаемым данным, моделируя данные из этих распределений и затем сделать выводы, основанные на моделировании, например, определить процент дефектов и т. д. Компоненты дисперсии и смешанная модель ANOVA/ANCOVA
В модуле Компоненты дисперсии можно анализировать планы с любой комбинацией фиксированных эффектов, случайных эффектов и ковариат. Могут быть эффективно проанализированы очень большие планы: факторы могут иметь несколько сотен уровней. Программа способна анализировать как стандартные факторные (перекрестные), так и иерархически вложенные планы, и вычисляет стандартные суммы квадратов и средние квадраты I, II и III типов для эффектов модели. Кроме того, можно вычислить таблицу ожидаемых средних квадратов для эффектов плана, компоненты дисперсии для случайных эффектов модели, коэффициенты для синтеза знаменателя и полную таблицу дисперсионного анализа с критериями, основанными на суммах квадратов для синтезированных ошибок и числе степеней свободы. Реализованы также другие методы оценки компонент дисперсии (MIVQUE0, максимума правдоподобия [МП] и ограниченного максимума правдоподобия). При оценке методом максимума правдоподобия применяются алгоритмы Ньютона-Рафсона и Фишера, при оценивании модель не изменяется (не сокращается) принудительным образом, чтобы справляться с ситуациями, когда большинство компонент близки к нулю. Имеется ряд функций для просмотра взвешенных и невзвешенных маргинальных средних и их доверительных интервалов. Для визуализации результатов реализованы разнообразные графические средства. Анализ выживаемости
В модуле реализованы также процедуры подгонки различных типов функций выживания (включая экспоненциальную, линейного риска, Гомпертца и Вейбулла) по методу невзвешенных или взвешенных наименьших квадратов (оценки максимума правдоподобия для параметров различных распределений, включая распределение Вейбулла, можно вычислять также в модуле Анализ процессов STATISTICA). Наконец, в программе в полном объеме реализованы четыре общие объясняющие модели (модель пропорциональных интенсивностей Кокса, экспоненциальная регрессионная модель, нормальная и лог-нормальная регрессионные модели) с расширенной диагностикой, включающей стратифицированный анализ и графики выживаемости для заданных пользователем значений предикторов. В регрессионной модели пропорциональных интенсивностей Кокса пользователь может решить, стратифицировать ли выборку, чтобы сделать возможным задание разных базовых функций интенсивности для разных слоев (но с общим вектором коэффициентов), или же допускать как различные базовые функций интенсивности, так и различные векторы коэффициентов. Кроме того, имеются средства для задания одной или нескольких зависящих от времени ковариат. Такие ковариаты задаются с помощью удобного формульного редактора через арифметические выражения, которые могут явным образом содержать время, все обычные логические операции (пример: timdep=age+age*log(t_)*(age>45); здесь t_ – время жизни), а также различные распределения. Как и во всех других модулях системы STATISTICA, пользователь может изменять технические параметры всех процедур (или принять динамически определяемые значения по умолчанию). Интерпретировать результаты помогают реализованные в модуле многочисленные виды графиков и специализированных диаграмм (диаграммы накопленных долей выживаний/отказов, структуры цензурированных данных, графики функции риска (обычный и кумулятивный) и плотности вероятности, сравнительные диаграммы для групп, графики подгонки распределений, различные графики остатков и другие). Модели пропорциональных рисков Кокса
Эта модель стала очень популярна во многих областях, где зависимая интересующая переменная представляет время наступления определенного события, а время проведения наблюдений и анализа ограничено, например:
Модуль Модель пропорциональных рисков Кокса позволяет эффективно работать с цензурированными данными, категориальными предикторами и планами, содержащими взаимодействия и/или вложенные эффекты. В качестве техники построения моделей этот модуль использует метод наилучших подмножеств и пошаговую регрессию. Построение функций выживаемости для новых данных можно задать с помощью STATISTICA Rapid Deployment. Общее нелинейное оценивание (включая логит/пробит регрессию)
Методы оцениванияМодель может подгоняться по методу наименьших квадратов, по критерию максимума правдоподобия или с помощью любой определенной пользователем функции потерь. Имеется возможность выбрать один из четырех мощных, и существенно различных по своим характеристикам методов оценивания (квази-ньютоновский, симплекс-метод, метод Хука-Дживиса и метод Розенброка), так что практически в любой задаче (даже очень сложной в вычислительном отношении) можно получить устойчивые оценки параметров. МоделиПользователь может задать произвольный тип модели, вводя соответствующее уравнение в специальное окно редактора. Уравнения могут включать логические операторы, поэтому имеется возможность оценивать (кусочно-) разрывные модели регрессии и модели с индикаторами групп. В уравнениях могут быть использованы различные теоретические функции распределения (бета, биномиальное, Коши, хи-квадрат, экспоненциальное, экстремальных значений, F, гамма, геометрическое, Лапласа, логистическое, нормальное, логнормальное, Парето, Пуассона, Рэлея, t (Стьюдента) и Вейбулла). Пользователю предоставляется полный контроль над всеми аспектами процедуры оценивания (начальные значения, величина шага, критерий остановки итераций и т.д.). Наиболее распространенные нелинейные модели регрессии имеются в готовом виде в модуле Нелинейное оценивание и могут быть вызваны прямо из меню. В их числе – пошаговая пробит- и логит-регрессия, экспоненциальная и кусочно-линейная регрессия. Результаты
Для моделей логит и пробит автоматически производится пошаговая подгонка с добавлением/удалением параметров регрессионной модели (благодаря чему имеется возможность анализировать данные с помощью пошаговой процедуры нелинейного оценивания). В модуле Общие Линейные Модели (GLM) существуют опции для автоматизации прямой и обратной пошаговой регрессии. ГрафикиДля всех результатов реализованы разнообразные возможности графического представления, в том числе интерактивные двух- и трехмерные графики функции подгонки, с помощью которых можно визуально отслеживать качество подгонки, выявлять выбросы и наблюдать меру расхождения модели и данных; пользователь может интерактивно видоизменять уравнение функции подгонки без повторной обработки данных и визуализировать практически все этапы процедуры нелинейной подгонки. Для оценки качества подгонки и визуализации результатов имеются также различные специальные графические средства: гистограммы всех выбранных переменных и значений остатков, графики зависимости наблюдаемых значений от предсказанных и предсказанных от остаточных значений, нормальные и полунормальные вероятностные графики остатков и различные другие возможности. Логлинейный анализ
В модуле Логлинейный анализ можно анализировать таблицы с числом измерений до 7. Таблицы могут содержать структурные нули. Частотные таблицы могут быть вычислены по исходным данным либо введены непосредственно. Реализованный в модуле Логлинейный анализ универсальный набор мощных методов моделирования в сочетании с гибким интерактивным интерфейсом принципиально упрощает проведение разведочного и подтверждающего анализа сложных таблиц. В любой момент пользователь имеет возможность просмотреть всю наблюдаемую таблицу целиком и маргинальные таблицы, подогнанные (ожидаемые) значения, оценить качество подгонки для всех ассоциированных частных и маргинальных моделей и выбрать для подгонки к данным специфическую модель (маргинальную таблицу). Для выбора модели в программе реализована автоматическая система интеллектуальной поддержки; сначала она определяет нужный порядок взаимодействия, обеспечивающий подгонку модели к данным, а затем, путем обратного исключения, находит наилучшую из моделей, достаточно хорошо (в смысле заданного пользователем критерия) аппроксимирующую данные. В стандартный набор результатов входят: статистика G-квадрат (отношение максимального правдоподобия хи-квадрат) и стандартная статистика хи-квадрат Пирсона с соответствующим числом степеней свободы и уровнями значимости, наблюдаемая и подогнанная (ожидаемая) таблицы, маргинальные таблицы и другие статистики. Графические средства модуля Логлинейный анализ включают множество двух- и трехмерных диаграмм для визуального представления двух- и многовходовых частотных таблиц (в том числе - управляемые пользователем каскады категоризованных гистограмм и трехмерные гистограммы, показывающие "срезы" многовходовых таблиц). Кроме того, реализованы диаграммы наблюдаемых и подогнанных частот, диаграммы различных типов остатков (стандартизованные, компоненты отношения максимального правдоподобия хи-квадрат, отклонения Фримена-Тьюки и др.) и другие разнообразные средства. Анализ временных рядов и прогнозирование
Имеются самые разнообразные возможности для просмотра и графического представления одномерных и многомерных рядов. Можно анализировать очень длинные ряды (более 100 тыс. наблюдений). С многомерными рядами (в случае многомерных исходных данных или с рядами, полученными на различных этапах анализа) можно работать в активной рабочей области; здесь их можно просматривать и сопоставлять друг с другом. Программа автоматически отмечает все этапы анализа временного ряда и сохраняет полную историю преобразований и полученные результаты (остатки модели АРПСС, сезонную составляющую и т.д.). Поэтому пользователь всегда имеет возможность вернуться к более раннему этапу анализа или отобразить на графике исходный ряд и его преобразования. Информация о последовательных преобразованиях хранится в виде длинных меток переменных, поэтому при сохранении вновь полученных рядов в файле данных автоматически сохраняется вся "история" каждого из рядов. Далее описываются конкретные процедуры модуля Временные ряды. С помощью различных преобразований исходного временного ряда можно понять его структуру и имеющиеся в нем закономерности; в модуле реализованы такие часто используемые преобразования, как: удаление тренда, удаление автокорреляций, сглаживание скользящими средними (невзвешенными или взвешенными - с весами, заданными пользователем или вычисленными по методам Даниеля, Тьюки, Хэмминга, Парзена и Бартлета), медианное сглаживание (среднее заменено медианой), простое экспоненциальное сглаживание (подробное описание его вариантов см. далее), взятие разностей, суммирование, вычисление остатков, сдвиг, 4253H-сглаживание, косинус-сглаживание, преобразование Фурье, а также обратное преобразование Фурье и др. Можно выполнить анализ автокорреляций, частных автокорреляций и кросскорреляций. АРПСС и анализ прерванных временных рядов (рядов с интервенциями)Модуль Временные ряды включает полную реализацию модели авторегрессии и проинтегрированного скользящего среднего (АРПСС). Модель может включать константу. Перед построением модели ряд может быть подвергнут преобразованию, которое автоматически будет отменено после построения прогноза по АРПСС, при этом предсказанные значения и их стандартные ошибки будут выражены через значения исходного (а не преобразованного) ряда. Могут быть вычислены приближенные и точные суммы квадратов из условия максимума правдоподобия; уникальной особенностью модели АРПСС модуля Временные ряды является способность анализировать модели с длинными периодами сезонности (с лагом до 30). Стандартный набор результатов содержит оценки параметров, стандартные ошибки и корреляции. Предсказанные значения могут быть представлены в числовой и графической форме и добавлены к исходному ряду. Имеются многочисленные дополнительные функции для исследования остатков модели АРПСС, в том числе большой набор графических средств. Реализация модели АРПСС в модуле Временные ряды позволяет проводить анализ прерванных временных рядов (рядов с интервенциями). Имеется возможность использовать одновременно несколько различных интервенций (до 6). Доступны следующие виды интервенций: однопараметрические скачкообразные, двупараметрические постепенные, временные (характер воздействия можно просмотреть на графике). Для всех прерванных моделей могут быть построены прогнозы, которые можно вывести на график (вместе с исходным рядом) и, если требуется, добавить к исходному ряду. Сезонное и несезонное экспоненциальное сглаживаниеВ модуле Временные ряды полностью реализованы все 12 классических моделей экспоненциального сглаживания. Задание модели может включать аддитивную или мультипликативную сезонную составляющую и/или линейный, экспоненциальный или демпфированый тренд; в частности, доступны популярные модели с линейным трендом Холта-Винтера. Пользователь может задавать начальное значение параметров сглаживания, начальное значение тренда и (если требуется) сезонные факторы. Для тренда и сезонной составляющей могут быть заданы независимые параметры сглаживания. Для определения лучшей комбинации параметров используется метод поиска на сетке; в таблицах результатов для всех комбинаций значений параметров сглаживания вычисляется средняя ошибка, средняя абсолютная ошибка, сумма квадратов ошибок, среднеквадратическая ошибка, средняя относительная ошибка и средняя абсолютная относительная ошибка. Наименьшие значения этих ошибок выделяются цветом. Имеется возможность автоматического поиска лучшего набора параметров в смысле среднеквадратической, средней абсолютной или средней абсолютной относительной ошибки (для этого используется общая процедура минимизации). Все результаты преобразования экспоненциальным сглаживанием, остатки и прогноз на требуемое число шагов можно в дальнейшем проанализировать и изобразить на графике. Для оценки адекватности модели используются графики, на которых вместе с исходным рядом в подходящем масштабе по оси Y изображаются его сглаженный вариант, прогноз и ряд остатков. Классическая сезонная декомпозиция (метод Census I)Имеется возможность задать произвольный сезонный лаг и выбрать либо аддитивную, либо мультипликативную сезонную модель. Программа вычисляет скользящие средние, отношения или разности, сезонные компоненты, ряд с сезонной поправкой, сглаженную тренд-циклическую и нерегулярную компоненты. Все эти составляющие ряда доступны для дальнейшего анализа; например, для проверки адекватности можно построить гистограммы, нормальные вероятностные графики и т.д. Месячная и квартальная сезонная X-11-декомпозиция и корректировка (метод Census II)Модуль Временные ряды включает полную реализацию метода X-11 сезонной корректировки, принятого Статистическим управлением США (US Bureau of the Census). Структура всех функций и диалоговых окон соответствует требованиям и соглашениям, описанным в документации Bureau of the Census. Можно выбрать либо аддитивные, либо мультипликативные модели. Пользователь может дополнительно вычислить априорные поправки на число рабочих дней и сезонные поправки. Колебания числа рабочих дней оцениваются регрессионными методами (с правильной обработкой крайних членов ряда) и затем (по желанию) используются для корректировки ряда. Реализованы стандартные средства для градуировки выбросов, вычисления сезонных факторов и вычисления тренд-циклической компоненты (имеется возможность выбирать несколько типов взвешенного скользящего среднего; кроме того, программа может сама находить оптимальную длину и тип скользящего среднего). Итоговые компоненты ряда (сезонная, тренд-циклическая, нерегулярная) и ряд с внесенной сезонной поправкой всегда доступны для дальнейшего анализа и вывода на график; кроме того, все они могут быть сохранены для дальнейшего исследования другими методами и/или в других программах. Все компоненты выводятся на графики в различной форме, включая категоризованные графики по месяцам (кварталам). Полиномиальные модели распределенных лаговС помощью реализованных в модуле Временные ряды методов анализа полиномиальных распределенных лагов можно выполнять оценку моделей с обычными лагами и лагами Алмона. Для анализа распределений переменных модели имеется ряд графических средств. Спектральный (Фурье) анализ и кросс-спектральный анализМодуль Временные ряды включает полную реализацию методов спектрального или Фурье анализа одного ряда и кросс-спектральный анализ двух рядов. Преимущества реализации спектрального анализа в STATISTICA особенно отчетливо проявляются при анализе очень длинных временных рядов (с более чем 250 тыс. наблюдений) и не предполагают каких-либо ограничений на длину ряда (в частности, длина исходного ряда не обязательно должна быть четной). Вместе с тем, иногда бывает разумно предварительно увеличить или уменьшить длину ряда. Стандартные методы предварительной обработки ряда включают косинус-сглаживание, вычитание среднего и удаление тренда. Результаты обычного спектрального анализа содержат коэффициенты частоты, периода, коэффициенты при синусах и косинусах, периодограммы и оценку спектральной плотности. Оценка плотности может быть вычислена с помощью весов Даниеля, Хэмминга, Бартлетта, Тьюки, Парзена или с весами и шириной, заданными пользователем. Очень полезно, особенно при работе с длинными рядами, иметь возможность выводить в убывающем порядке заранее заданное число точек периодограммы или спектральной плотности; таким образом можно легко обнаружить резкие пики периодограммы и спектральной плотности для длинных рядов. Имеется возможность вычислить d-критерий Колмогорова-Смирнова для значений периодограммы, чтобы проверить, подчиняются ли они экспоненциальному распределению (является ряд белым шумом или нет). Для представления результатов анализа имеются различные типы графиков; можно отобразить коэффициенты при синусах и косинусах, периодограмму, лог- периодограмму, спектральную и лог-спектральную плотность по отношению к частотам, периодам и лог- периодам. В случае длинного исходного ряда имеется возможность выбрать конкретный сегмент (период), для которого будут изображаться соответствующие периодограмма и график спектральной плотности, тем самым будет улучшено их "разрешение". При кросс-спектральном анализе, в дополнение к результатам обычного спектрального анализа каждого отдельного ряда, вычисляется кросс-периодограмма (вещественная и мнимая часть), ко-спектральная плотность, квадратурный спектр, кросс-амплитуда, значения когерентности, усиления и фазовый спектр. Все эти величины могут быть выведены на график, где по горизонтальной оси будет откладываться частота, период или лог-период либо для всего интервала периодов (соответственно, частот), либо для выбранного пользователем диапазона. Указанное пользователем количество наибольших значений кросс-периодограммы (вещественных или мнимых) может быть выведено в убывающем порядке в виде таблицы результатов, что позволяет легко выявлять на ней резкие пики для длинных исходных рядов. Как и во всех других процедурах модуля Временные ряды, все полученные ряды могут быть добавлены в активную рабочую область и затем подвергнуты дальнейшему исследованию с помощью других методов анализа временных рядов или средствами других модулей системы STATISTICA. Прогнозирование на основе регрессионных методовНаконец, в системе STATISTICA реализованы регрессионные методы анализа временных рядов для переменных с запаздыванием (лагом) или без него, в том числе регрессия, проходящая через начало координат, нелинейная регрессия и интерактивное прогнозирование по методу "что-если". Моделирование структурными уравнениями (SEPATH)В системе STATISTICA в полном объеме реализованы методы моделирования с помощью структурных уравнений и гибкие средства имитационного моделирования методом Монте-Карло. В модуль SEPATH вошли самые последние разработки в этой области, объединенные "интеллектуальным" пользовательским интерфейсом. Здесь представлен широкий выбор процедур моделирования, а уникальные средства интерфейса позволяют строить даже чрезвычайно сложные модели, не обращаясь ни к какому командному языку. С помощью Мастера структурного моделирования и Конструктора путей можно задать все процедуры анализа в простых функциональных терминах через меню и диалоговые окна (в отличие от других программ моделирования структурными уравнениями, здесь нет необходимости изучать специальный и достаточно сложный "язык"). Модуль SEPATH представляет собой полную реализацию этого класса методов и содержит целый ряд дополнительных возможностей: например, есть возможность проанализировать матрицы корреляций, ковариаций и моментов (в моделях со структурированными средними и константами); построить модель можно средствами Мастера путей, Мастера факторного анализа и Конструктора путей. Эти высокоэффективные средства позволяют за считанные минуты определять сложнейшие модели, выбирая варианты в диалоговых окнах. Используя методы условной оптимизации, программа SEPATH вычисляет стандартные ошибки для стандартизованных моделей и моделей, подогнанных к корреляционным матрицам. В качестве результатов выдается набор диагностических статистик (в том числе стандартные и нецентральные индексы подгонки), отражающий все последние достижения в области моделирования структурными уравнениями. Имеется возможность подгонять модель к нескольким выборкам (группам) и задавать для каждой группы фиксированные, свободные или связанные (одинаковые для всех групп) параметры. При анализе матрицы моментов эти средства позволяют проверять сложные гипотезы о структурных средних для различных групп. Документация к модулю SEPATH содержит подробные описания большого числа примеров, взятых из литературы, в том числе примеры подтверждающего факторного анализа, анализа путей, модели теории тестирования для подобных тестов, матрицы моделей с несколькими уровнями реакции испытуемых, продольную факторную модель, сложную симметрию, структурированные средние и др. Имитационное моделирование по методу Монте-Карло в модуле SEPATHМодуль Моделирование структурными уравнениями (SEPATH) системы STATISTICA содержит мощные средства имитационного моделирования методом Монте-Карло: имеется возможность порождать (и сохранять) наборы данных для предопределенных моделей, основанных на нормальном распределении или на скошенных распределениях. С помощью метода Монте-Карло можно вычислять оценки с помощью бутстрепа, распределения различных информационных статистик, оценки параметров и т.д. Для визуализации результатов метода Монте-Карло (например, распределений параметров) служат различные графические средства. Общие линейные модели (GLM)Модуль Общие Линейные Модели STATISTICA (GLM) предназначен для анализа откликов одной или нескольких непрерывных переменных как функции одной или нескольких категориальных или непрерывных независимых переменных. GLM является не только вычислительным средством, но также и наиболее удобным и полным из доступных приложений, предоставляющим широкий выбор опций, графиков, сопутствующих статистик и расширенных диагностических функций. STATISTICA GLM предлагает наиболее богатые опции для поддержки GLM-спорных задач, для которых не существует стандартных решений. GLM вычисляет все стандартные результаты, включая ANOVA-таблицы с одномерными и многомерными тестами, описательными статистиками и т.п. GLM предлагает широких выбор результатов и графических опций, которые обычно не доступны в других программах. GLM также предлагает простые способы тестирования линейных комбинаций параметров оценивания, спецификации пользовательских членов ошибки и эффектов, расширенные апостериорные методы сравнения межгрупповых эффектов, повторные эффекты измерений и взаимодействий между повторными измерениями. Общие регрессионные модели (GRM)Общие регрессионные модели STATISTICA (GRM) предлагают пользователю уникальную высоко эффективную реализацию стандартных функций в общей линейной модели, а также включают широкий набор пошаговой регрессии и технологии лучшего подмножества построения моделей, поддерживающие непрерывные и категориальные переменные. Пошаговые методы и методы лучшего подмножества построения моделей составных планов можно использовать в GRM, включая планы с эффектами для категориальных предсказанных переменных. GRM не ограничивает анализы в плане содержания непрерывных предсказанных переменных. Кроме этого, исключительные опции регрессионных результатов включают карты Парето параметров оценивания, целые модельные критерии с различными методами оценивающих моделей, частные и получастные корреляции и т.п. Обобщенные линейные модели (GLZ)Модуль Обобщенные линейные модели (GLZ) позволяет анализировать как линейные, так и нелинейные эффекты для любого количества и типа предикторов с дискретной или непрерывной зависимой переменной (включая множественную логит, пробит модели, распознавание сигналов и многие другие). Кроме того, в этом модуле реализованы разнообразные типы анализов, такие как биномиальная и множественная логит и пробит регрессия или Теория определения сигнала (SDT). Модуль GLZ вычислит все стандартные итоговые статистики, включая критерии оценки правдоподобия, статистики Вальда для значимых эффектов, оценки параметров, их стандартные ошибки, доверительные интервалы и т.д. Интерфейс, способы задания плана и использование программы аналогичны модулям GLM, GRM и PLS. Пользователь может легко задать ANOVA или ANCOVA-подобные планы, планы поверхности отклика, смешанные планы и т.д.; поэтому, даже у новичков не возникнет трудностей с применением обобщенных линейных моделей к анализу данных. Кроме того, модуль GLZ предоставляет обширный выбор инструментов проверки модели, таких как таблицы и графики различных статистик остатков или выбросов (включая исходные остатки, остатки Пирсона, сумму квадратов остатков, стьюдентизированные остатки Пирсона, стьюдентизированные суммы квадратов остатков, остатки правдоподобия, дифференциальные статистики Хи-квадрат, дифференциальную сумму квадратов, обобщенные расстояния Кука и т. д. Общие модели частных наименьших квадратов (PLS)Модуль Общие модели частных наименьших квадратов (PLS) представляет обширный выбор алгоритмов для решения одномерных и многомерных задач по методу частных наименьших квадратов. PLS вычисляет все стандартные результаты, как для анализа частных наименьших квадратов. Также, в этом модуле представлено множество средств интерпретации результатов и, в частности, графического представления данных, которые обычно не доступны в других приложениях. Например, Вы можете воспользоваться такими опциями, как график значений параметра как функции числа компонент, двухмерные графики для всех входных статистик (параметров, факторов и т.д.), двухмерные графики для всех статистик остатков и т.д. Поскольку модуль PLS аналогичен по своему интерфейсу модулям GLM, GRM и GLZ, для Вас не составит трудности построить модель в одном модуле и быстро проанализировать данные с помощью этой же модели в PLS. Уникальный гибкий интерфейс позволит даже начинающим пользователям использовать эти мощные инструменты для анализа своих задач. Метод частных наименьших квадратов – это мощная технология добычи данных, особенно хорошо подходит для нахождения меньшего количества размерностей в большом количестве предикторов или переменных отклика. Подобные методы анализа линейных систем стали популярны только в последние несколько лет, поэтому многие алгоритмы и статистики по-прежнему находятся на стадии исследования. STATISTICA Multivariate Exploratory Techniques (Многомерные технологии анализа данных)Модуль Многомерные разведочные технологии анализа STATISTICA предоставляет широкий выбор разведочных технологий, начиная с кластерного анализа до расширенных методов классификационных деревьев, в сочетании с огромным набором средств интерактивной визуализации для построения моделей. В состав модуля входят:
Методы кластерного анализа
Матрицы расстояний можно сохранять для дальнейшего анализа в других модулях системы STATISTICA. При проведении кластерного анализа методом k-средних пользователь имеет полный контроль над начальным расположением центров кластеров. Могут быть выполнены чрезвычайно большие планы анализа: так, например, при иерархическом (древовидном) связывании можно работать с матрицей из 90 тыс. расстояний. Помимо стандартных результатов кластерного анализа, в модуле доступен также разнообразный набор описательных статистик и расширенных диагностических методов (полная схема объединения с пороговыми уровнями при иерархической кластеризации, таблица дисперсионного анализа при кластеризации методом k-средних). Информация о принадлежности объектов к кластерам может быть добавлена к файлу данных и использоваться в дальнейшем анализе. Графические возможности модуля Кластерный анализ включают настраиваемые дендрограммы, двухвходовые диаграммы объединений, графическое представление схемы объединения, диаграмму средних при кластеризации по методу k-средних и многое другое. Факторный анализ и анализ главных компонент
Анализ главных компонент и классификацияSTATISTICA также включает программу для анализа главных компонент и классификации. Выходные результаты этой программы – собственные значения (обычные, кумулятивные и относительные), нагрузки факторов и коэффициенты факторных баллов (которые можно добавить к файлу входных данных, просмотреть на пиктографике и в интерактивном режиме перекодировать), а также некоторые более специальные статистики и диагностики. В распоряжении пользователя имеются следующие методы вращения факторов: варимакс, биквартимакс, квартимакс и эквимакс (по нормализованным либо первоначальным нагрузкам), а также косоугольные вращения. Пространство факторов можно визуально просматривать "срез за срезом" на двух- или трехмерных диаграммах рассеяния с отмеченными точками данных; среди других графических средств - графики "каменистой осыпи", различные типы диаграмм рассеяния, гистограммы, линейные графики и др. После того, как факторное решение определено, пользователь может вычислить (воспроизвести) корреляционную матрицу и оценить согласованность факторной модели путем анализа остаточной корреляционной матрицы (или остаточной дисперсионной/ковариационной матрицы). На входе можно использовать как исходные данные, так и матрицы корреляций. Подтверждающий факторный анализ и другие, связанные с ним виды анализа, могут быть выполнены средствами модуля Моделирование структурными уравнениями (SEPATH) из блока STATISTICA Общие Линейные и Нелинейные Модели, где специальный Мастер подтверждающего факторного анализа проведет пользователя через все этапы построения модели. Канонический анализ
В модуле Каноническая корреляция имеется большой набор графических средств (включая диаграммы собственных значений и канонических корреляций, диаграммы значений канонических переменных и много других). Подтверждающий анализ структурных связей между латентными переменными может быть также выполнен средствами модуля Моделирование структурными уравнениями (SEPATH). Надежность и позиционный анализ
Имеется возможность вычислять статистики надежности для всех позиций шкалы, интерактивно выбирать подмножества и проводить сравнение между подмножествами позиций методом разбиения пополам ("split-half") или на две части ("split-part"). За одно обращение можно оценить надежность суммарной шкалы и подшкал. При интерактивном удалении позиций надежность результирующей шкалы вычисляется мгновенно без повторного обращения к файлу данных. В качестве результатов анализа выдаются: корреляционные матрицы и описательные статистики для позиций, альфа Кронбаха, стандартизованное альфа, средняя корреляция позиция-позиция, полная таблица дисперсионного анализа для шкалы, полный набор статистик, общих для всех позиций (включая коэффициенты множественной корреляции), split-half-надежность и корреляция между двумя половинками с поправкой на затухание. Имеется большой выбор графиков (включая встроенные диаграммы рассеяния, гистограммы, линейные и другие графики) и набор интерактивных процедур что-если, помогающих при разработке шкал. Например, при добавлении некоторого количества вопросов в шкалу пользователь может вычислить ожидаемую надежность или же оценить количество вопросов, которые нужно внести в шкалу, чтобы добиться нужной надежности. Кроме того, можно внести поправку на затухание между текущей шкалой и другим измерением (при заданной надежности текущей шкалы). Деревья классификации
В модуле также реализованы: выбор между полным перебором вариантов ветвления (как в пакетах THAID и CART) и дискриминантным ветвлением; несмещенный выбор переменных ветвления (как в пакете QUEST); явное задание правил остановки (как в пакете FACT) или отсечение от листьев дерева к его корню (как в пакете CART); отсечение по доле ошибок классификации или по функции отклонения; обобщенные меры согласия хи-квадрат, G-квадрат и индекс Джини. Априорные вероятности принадлежности классам и цены ошибок классификации можно положить равными, оценить по данным или задать вручную.
Анализ соответствий
В процессе работы программа вычисляет различные таблицы, в том числе таблицу процентов по строкам, по столбцам и процентов от общего числа, ожидаемые значения, разности ожидаемых и наблюдаемых значений, стандартизованные отклонения и вклады в статистику хи-квадрат. Все эти статистики можно изобразить на трехмерных гистограммах и просмотреть с помощью специального метода динамического расслоения. В модуле Анализ соответствий вычисляются обобщенные собственные значения и собственные векторы, и выдается стандартный набор диагностических величин, включающий сингулярные числа, собственные значения и долю инерции, приходящуюся на каждое измерение. Пользователь может либо сам выбрать число измерений, либо задать пороговое значение для максимального кумулятивного процента инерции. Программа вычисляет стандартные координаты для точек-строк и точек-столбцов. Пользователь может выбрать между стандартизацией по профилям строк, по профилям столбцов, по профилям строк и столбцов или каноническую стандартизацию. Для каждой размерности и для каждой точки-строки и точки-столбца программа вычисляет величины инерции, качества и косинус**2. Дополнительно пользователь может вывести (в окно результатов) матрицы обобщенных сингулярных векторов. Как и любые данные из рабочего окна, эти матрицы доступны для обработки с помощью программ на языке STATISTICA Visual Basic, например, для использования каких-либо нестандартных методов вычисления координат. Пользователь может вычислить координаты и соответствующие статистики (качество и косинус**2) для дополнительных точек (-столбцов или -строк) и сравнить результаты с исходными точками-строками и точками-столбцами. В многомерном анализе соответствий могут использоваться дополнительные точки. Помимо трехмерных гистограмм, которые могут быть вычислены для всех таблиц, пользователь может вывести на экран график собственных чисел, одно-, двух- и трехмерные диаграммы для точек-строк и точек-столбцов. Точки-строки и точки-столбцы могут отображаться одновременно на одной диаграмме вместе с любыми дополнительными точками (каждый тип точки использует свой цвет и уникальный маркер, так что различные точки будут легко различимы на диаграммах). Все точки имеют маркеры, и пользователь имеет возможность устанавливать размер маркера. Многомерное шкалирование
Пользователь имеет возможность наблюдать итерации и следить за изменениями этих значений. Окончательную конфигурацию можно просмотреть в таблице результатов, а также на двух- и трехмерных диаграммах рассеяния в пространстве шкал с отмеченными точками-объектами. В качестве выходных результатов выдаются: нестандартизованный стресс (F), коэффициент стресса Краскела S и коэффициент отчуждения. Уровень согласия может быть оценен с помощью диаграмм Шепарда (с величинами "d с крышкой" и "d со звездочкой"). Как и все результаты анализа в системе STATISTICA, окончательная конфигурация может быть сохранена в виде файла данных. Дискриминантный анализ
Программа позволяет проводить анализ с пошаговым включением или исключением переменных или вводить в модель заданные пользователем блоки переменных. В дополнение к многочисленным графикам и статистикам, описывающим разделяющую (дискриминирующую) функцию, программа содержит также большой набор средств и статистик для классификации старых и новых наблюдений (для оценки качества модели). В качестве результатов выдаются: статистика лямбда Уилкса для каждой переменной, частная лямбда, статистика F для включения (или исключения), уровни значимости p, значения толерантности и квадрата коэффициента множественной корреляции. Программа выполняет полный канонический анализ и выдает все собственные значения (в непосредственном виде и кумулятивные), их уровни значимости p, коэффициенты дискриминантной (канонической) функции (в непосредственном и стандартизованном виде), коэффициенты структурной матрицы (нагрузки факторов), средние значения дискриминантной функции и дискриминантные веса для каждого объекта (их можно автоматически добавить в файл данных). Встроенные средства графической поддержки включают: гистограммы канонических весов для каждой группы (и общие по всем группам), специальные диаграммы рассеяния для пар канонических переменных (на которых отмечено, к какой группе принадлежит каждое наблюдение), большой набор категоризованных (множественных) графиков, позволяющий исследовать распределение и взаимосвязи между зависимыми переменными для разных групп (в том числе: множественные графики типа диаграмм размаха, гистограммы, диаграммы рассеяния и нормальные вероятностные графики) и многое другое. В модуле Дискриминантный анализ можно также вычислить стандартные функции классификации для каждой группы. Результаты классификации наблюдений можно вывести в терминах расстояний Махаланобиса, апостериорных вероятностей и собственно результатов классификации, а значения дискриминантной функции для отдельных наблюдений (канонические значения) можно просмотреть на обзорных пиктографиках и других многомерных диаграммах, доступных непосредственно из таблиц результатов. Все эти данные можно автоматически добавить в текущий файл данных для дальнейшего анализа. Можно вывести также итоговую матрицу классификации, где указано число и процент правильно классифицированных наблюдений. Имеются различные варианты задания априорных вероятностей принадлежности классам, а также условий отбора, позволяющих включать или исключать определенные наблюдения из процедуры классификации (например, чтобы затем проверить ее качество на новой выборке). Общие модели дискриминантного анализа (GDA)Модуль Общие модели дискриминантного анализа STATISTICA (GDA) является приложением и расширением Общих Линейных Моделей для классификации задач. Также как и модуль Дискриминантный Анализ, GDA позволяет выполнять обычные последовательные дискриминантные анализы. GDA представляет задачу дискриминантного анализа, как специальный случай общей линейной модели и, таким образом, предоставляет чрезвычайно полезные новые пользовательские аналитические технологии. Также как и обычный дискриминантный анализ, GDA позволяет выбрать нужные категории зависимых переменных. В анализе группы элементов записаны в виде индикаторных переменных, и можно легко применять все методы GRM. В диалоге результатов GDA доступен широкий выбор остаточных статистик GRM и GLM. GDA предоставляет разнообразные эффективные средства для добычи данных и прикладных исследований. GDA вычисляет все стандартные результаты дискриминантного анализа, включая коэффициенты дискриминантной функции, канонические результаты анализа (стандартизованные и необработанные коэффициенты, пошаговые тесты канонических корней и т. п.), классификационные статистики (включая, расстояние Махаланобиса, апостериорные вероятности, классификацию наблюдений в допустимых анализах, матрицы ошибочной классификации и т. п.). STATISTICA Power Analysis and Interval Estimation (Анализ мощности и интервальное оценивание)Общий обзор
С другой стороны, использование слишком большой выборки затруднено с технической стороны. STATISTICA Анализ мощности поможет подобрать оптимальный размер выборки и пополнит Ваш набор инструментов для оценивания доверительных интервалов и проведения всестороннего анализа мощности Вы всё ещё не убеждены в необходимости использования этого модуля? Прочтите подробное техническое описание STATISTICA Анализ мощности... Подробное описаниеАнализ мощности STATISTICA является всесторонним инструментом для планирования Ваших исследований. Он помогает найти подходящий размер выборки для вашего конкретного анализа. В модуле представлен широкий спектр функций для анализа статистической мощности и вычисления размера выборки. Почему модуль Анализ мощности STATISTICA наиболее современное и мощное средство в своей области?
Перечень критериевВычисление размера выборкиАнализ мощности STATISTICA во всех ниже перечисленных критериях вычисляет размер выборки как функцию от ошибки первого рода и стандартного отклонения. Анализ мощности STATISTICA вычисляет мощность как функцию от размера выборки, стандартного размера и ошибки первого рода для критериев:
Вычисление доверительных интерваловСовременные статистические процедуры основаны на теории доверительных интервалов. Анализ мощности STATISTICA – уникальная программа в своем роде, которая вычисляет доверительные интервалы для множества статистических величин, таких как стандартизованный размер эффекта (в t-критерии и ANOVA), корреляционный коэффициент, квадрат составной корреляции, пропорция выборки, различие между пропорциями (как для зависимых и независимых выборок). Эти возможности можно использовать для построения доверительных интервалов для таких величин, как мощность и размер выборки, при этом позволяя пользователю использовать данные из одного исследования для построения точных доверительных интервалов требуемого размера выборки в другом исследовании. Калькуляторы статистического распределенияКроме широкого спектра распределений доступных во всех модулях STATISTICA, модуль Анализ мощности STATISTICA предоставляет специальные возможности, которые достаточно полезны при проведении мощных вычислений. Эти процедуры включают нецентральное t, нецентральное F, нецентральное хи-квадрат, хи-квадрат, биномиальное распределение коэффициента корреляции и точное распределение квадрата составного коэффициента корреляции, которые можно вычислять для неизвестных параметров, а также для обработки "ненулевых" наблюдений. Например, при вычислении корреляции Пирсона можно находить не только значения р, как функции от r и N при rho=0, но и для других значений rho, при попадании наблюдаемого r в конкретную процентную точку, при любом N. 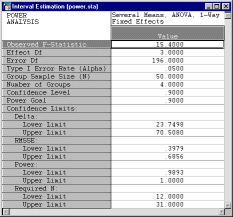
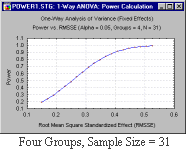
Пример приложения. Рассмотрим задачу проведения 1-факторного Дисперсионного анализа при изучении эффекта наркотиков. Вначале рассмотрим результаты предварительного анализа. В данном анализе рассматривается 4 группы, в каждой из которых содержится N = 50 объектов, причем значение F-статистики равно 15.4. На первом шаге из полученной информации можно (a) оценить величину эффекта размерности при помощи доверительных интервалов, (b) использовать эту информацию для установки нижнего предела подходящего размера выборки в текущем исследовании. После ввода данных в соответствующем диалоговом окне, результаты появляются немедленно. На рисунке слева приведены результаты исследования. В данном примере мы получили, что 90-процентный доверительный интервал со среднеквадратичным стандартизованным эффектом лежит между .398 и .686. Для эффекта такой величины не удивительно, что 90% апостериорный доверительный интервал мощности находится в диапазоне от .989 до 1. Мы можем использовать эту информацию для построения доверительных интервалов реального размера N для достижения необходимой мощности (в нашем случае, .90). Доверительный интервал лежит между 12 и 31. Исходя из этого, мы можем быть уверены, что в 90% случаев размер выборки не превышает 31, имея при этом мощность, равную .90.
С другой стороны, возвращаясь к нашему анализу, рассмотрим связь между мощностью и эффектом размера для выборки объемом 31. 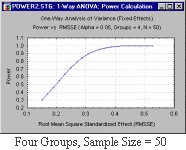
Первый график (справа) показывает достаточно точно, что пока эффект размера для исследуемого наркотика находится в доверительном интервале из предыдущего анализа, мощность будет достаточно высокой. Напротив, если мы сравним результаты полученного размера выборки с предыдущим анализом (например, 50 человек в группе), то обнаружим, что мощность остается достаточно умеренной, даже для эффектов порядка 0.28 (см. график справа). В Анализе мощности STATISTICA эта процедура занимает не более 1-2 минут. Был заказан постпроцессор на 5-ти координатный обрабатывающий центр. Работа выполнена с опережением срока. Большое спасибо за оперативность! В дальнейшем будем работать с Вами.
|
Консультации и прием заказов:
(495) no skype addon845-20-40, (812) no skype addon615-81-20
Что о нас говорят Клиенты?
25.04.2025
Дмитрий, г. Липецк
17 апреля 2025 года я приобрел годовую подписку на D5 Render. На следующий день мне пришел лицензионный ключ, который я успешно активировал через несколько дней. В процессе общения со службой поддержки мне ответили на все интересующие вопросы. Очень рекомендую этот сервис!
19.04.2025
Андрей, Архитектор, г. Белголод
Быстро и четко! Прямо таки спасли!Ключ выслали в тот же день оформления. Спасибо!
10.04.2025
Евгений, г. Москва
Большое спасибо Рамзану Казбекову. Всё четко, оперативно, отзывчиво.
Все отзывы >> Доставка
Программное обеспечение может поставляться как физически, так и средствами электронной связи. Доставка продукта, бухгалтерских и юридических документов, сертификатов, бумажных лицензий и т.д. осуществляется бесплатно по всей территории Российской Федерации.
Сроки на поставку регулируются компаниями-производителями и транспортной службой и оговариваются в каждом случае отдельно. Сроки доставки после комплектации на нашем складе до любой точки РФ редко превышают 2-3 рабочих дня.
О производителе
StatSoft Inc. на сегодняшний день является одним из крупнейших в мире разработчиков статистического и аналитического программного обеспечения. Программные продукты StatSoft поддерживаются глобальной сетью филиалов и дистрибуторов в разных странах и используются в основных университетах, корпорациях и правительственных учреждениях во всем мире.
Основной продукт компании – система STATISTICA, предназначенная для анализа данных, визуализации, прогнозирования и проведения многих других ст...
|
|
© «Архитект Дизайн» (ООО "Джазл"), 2006-2025 г. Все права защищены. Цены, указанные на сайте, являются ориентировочными. С условиями возврата приобретенного ПО Вы можете ознакомиться здесь. По всем вопросам обращайтесь: info@architect-design.ru, тел. 8-800-505-05-40, (495) 845-20-40, (812) 615-81-20. |
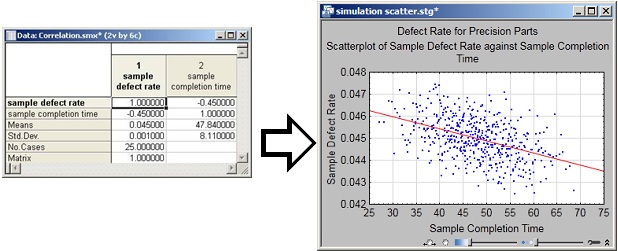 Модуль Подгонка и моделирование используется для оценки подгонки теоретических распределений к наблюдаемым данным. Кроме того, вы можете смоделировать данные из теоретического распределения с выбором внутренней корреляционной структуры данных. Кажущийся на вид простым, этот метод позволяет вам безошибочно смоделировать текущие процессы, создающие данные. Полученные данные с помощью этих процессов позволяют смоделировать и оценить работу системы.
Модуль Подгонка и моделирование используется для оценки подгонки теоретических распределений к наблюдаемым данным. Кроме того, вы можете смоделировать данные из теоретического распределения с выбором внутренней корреляционной структуры данных. Кажущийся на вид простым, этот метод позволяет вам безошибочно смоделировать текущие процессы, создающие данные. Полученные данные с помощью этих процессов позволяют смоделировать и оценить работу системы.  Модуль Компоненты дисперсии и смешанная модель ANOVA/ANCOVA предназначен для анализа смешанных моделей дисперсионного анализа со случайными факторами. Подобные факторы часто возникают в промышленных исследованиях (данный модуль входит также в пакет Промышленная
Модуль Компоненты дисперсии и смешанная модель ANOVA/ANCOVA предназначен для анализа смешанных моделей дисперсионного анализа со случайными факторами. Подобные факторы часто возникают в промышленных исследованиях (данный модуль входит также в пакет Промышленная  Этот модуль содержит широкий набор методов анализа цензурированных данных, применяемых в общественных науках, биологии, медицинских исследованиях, а также в маркетинге и технике (контроль качества, оценка надежности и др.). После вычисления таблиц времен жизни, различных описательных статистик и множительных оценок Каплана-Мейера пользователь может сравнить функции выживания по группам, используя для этого различные методы (критерий Гехана-Вилкоксона, F-критерий Кокса, критерий Кокса-Ментела, лог-ранговый критерий и обобщенный критерий Пето-Вилкоксона). Диаграммы Каплана-Мейера могут быть построены для отдельных групп (при этом нецензурированные наблюдения изображаются на графиках с помощью особых символов).
Этот модуль содержит широкий набор методов анализа цензурированных данных, применяемых в общественных науках, биологии, медицинских исследованиях, а также в маркетинге и технике (контроль качества, оценка надежности и др.). После вычисления таблиц времен жизни, различных описательных статистик и множительных оценок Каплана-Мейера пользователь может сравнить функции выживания по группам, используя для этого различные методы (критерий Гехана-Вилкоксона, F-критерий Кокса, критерий Кокса-Ментела, лог-ранговый критерий и обобщенный критерий Пето-Вилкоксона). Диаграммы Каплана-Мейера могут быть построены для отдельных групп (при этом нецензурированные наблюдения изображаются на графиках с помощью особых символов). 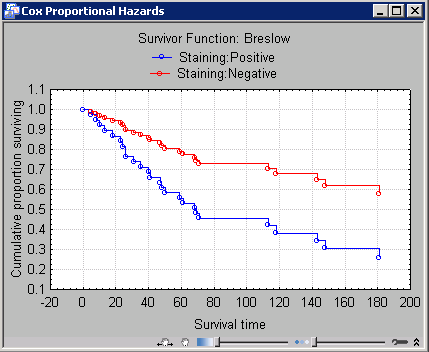 Основное отличие методов анализа выживаемости от классических методов анализа данных состоит в возможности использовать неполные (цензурированные) данные. Наблюдение считается цензурированным, если оно было изъято из исследования до наступления интересующего события. Для анализа такого типа данных многие модели, в том числе нормальная регрессия, непригодны.
Основное отличие методов анализа выживаемости от классических методов анализа данных состоит в возможности использовать неполные (цензурированные) данные. Наблюдение считается цензурированным, если оно было изъято из исследования до наступления интересующего события. Для анализа такого типа данных многие модели, в том числе нормальная регрессия, непригодны. В модуле Нелинейное оценивание реализованы методы, позволяющие осуществлять подгонку нелинейных моделей практически любого типа. Уникальная особенность этого модуля состоит в том, что (в отличие от обычных пакетов нелинейного оценивания) здесь нет никаких ограничений на размер обрабатываемого файла данных.
В модуле Нелинейное оценивание реализованы методы, позволяющие осуществлять подгонку нелинейных моделей практически любого типа. Уникальная особенность этого модуля состоит в том, что (в отличие от обычных пакетов нелинейного оценивания) здесь нет никаких ограничений на размер обрабатываемого файла данных.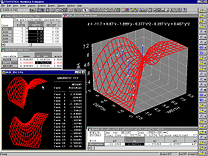 Помимо различных описательных статистик, в стандартный набор результатов нелинейного оценивания входят: оценки параметров и их стандартные ошибки (которые вычисляются независимо от самих оценок с помощью специальных повышающих точность конечно-разностных методов), матрица дисперсий/ковариаций для оценок параметров, предсказанные значения, остатки и соответствующие критерии согласия (лог-правдоподобие оцененной/нулевой моделей, критерий хи-квадрат для различий между средними, доля дисперсии, объясненная моделью, классификация наблюдений и отношение несогласия для моделей логит и пробит и др.). Предсказанные значения и остатки могут быть вставлены в файл данных для дальнейшего анализа.
Помимо различных описательных статистик, в стандартный набор результатов нелинейного оценивания входят: оценки параметров и их стандартные ошибки (которые вычисляются независимо от самих оценок с помощью специальных повышающих точность конечно-разностных методов), матрица дисперсий/ковариаций для оценок параметров, предсказанные значения, остатки и соответствующие критерии согласия (лог-правдоподобие оцененной/нулевой моделей, критерий хи-квадрат для различий между средними, доля дисперсии, объясненная моделью, классификация наблюдений и отношение несогласия для моделей логит и пробит и др.). Предсказанные значения и остатки могут быть вставлены в файл данных для дальнейшего анализа. 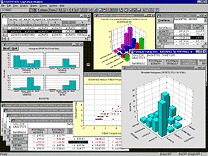 В этом модуле реализованы все процедуры логлинейного анализа многовходовых таблиц частот. Отметим, что
В этом модуле реализованы все процедуры логлинейного анализа многовходовых таблиц частот. Отметим, что 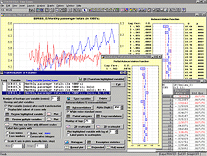 В модуле Временные ряды реализован широкий набор методов описания, построения моделей, декомпозиции и прогнозирования временных рядов, как во временной, так и в частотной области. Все процедуры полностью совместимы и результаты анализа одной модели (например, остатки, вычисленные для модели АРПСС) можно использовать для дальнейшего анализа (например, вычисления автокорреляции остатков).
В модуле Временные ряды реализован широкий набор методов описания, построения моделей, декомпозиции и прогнозирования временных рядов, как во временной, так и в частотной области. Все процедуры полностью совместимы и результаты анализа одной модели (например, остатки, вычисленные для модели АРПСС) можно использовать для дальнейшего анализа (например, вычисления автокорреляции остатков). 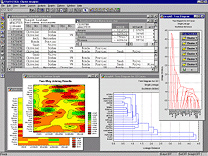 В модуле Кластерный анализ реализован полный набор методов кластерного анализа данных, включая методы k-средних, иерархической кластеризации и двухвходового объединения. Данные могут поступать как в исходном виде, так и в виде матрицы расстояний между объектами. Наблюдения, переменные или/и наблюдения, и переменные можно кластеризовать, используя различные меры расстояния (евклидово, квадрат евклидова, городских кварталов (манхэттеновское), Чебышева, степенное, процент несогласия и 1-коэффициент корреляции Пирсона) и различные правила объединения (связывания) кластеров (одиночная, полная связь, невзвешенное и взвешенное попарное среднее по группам, невзвешенное, взвешенное расстояние между центрами, метод Варда и другие).
В модуле Кластерный анализ реализован полный набор методов кластерного анализа данных, включая методы k-средних, иерархической кластеризации и двухвходового объединения. Данные могут поступать как в исходном виде, так и в виде матрицы расстояний между объектами. Наблюдения, переменные или/и наблюдения, и переменные можно кластеризовать, используя различные меры расстояния (евклидово, квадрат евклидова, городских кварталов (манхэттеновское), Чебышева, степенное, процент несогласия и 1-коэффициент корреляции Пирсона) и различные правила объединения (связывания) кластеров (одиночная, полная связь, невзвешенное и взвешенное попарное среднее по группам, невзвешенное, взвешенное расстояние между центрами, метод Варда и другие).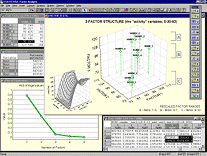 Модуль Факторный анализ содержит широкий набор статистик и методов факторного анализа (а также иерархического факторного анализа) с расширенной диагностикой и большим многообразием исследовательских и разведочных графиков. Здесь можно выполнять анализ (общий и иерархический косоугольный) главных компонент и главных факторов для наборов данных, содержащих до 300 переменных (модели большего объема можно исследовать средствами модуля Моделирование структурными уравнениями (SEPATH)).
Модуль Факторный анализ содержит широкий набор статистик и методов факторного анализа (а также иерархического факторного анализа) с расширенной диагностикой и большим многообразием исследовательских и разведочных графиков. Здесь можно выполнять анализ (общий и иерархический косоугольный) главных компонент и главных факторов для наборов данных, содержащих до 300 переменных (модели большего объема можно исследовать средствами модуля Моделирование структурными уравнениями (SEPATH)).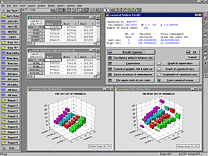 В этом модуле реализован полный набор методов канонического анализа (дополняющий методы канонического анализа, встроенные в другие модули). Работать можно как с файлами исходных данных, так и с корреляционными матрицами; вычисляются все стандартные статистики канонической корреляции (собственные векторы и собственные значения, коэффициенты избыточности, канонические веса, нагрузки, дисперсии, критерии значимости для каждого из корней и др.), а также некоторые расширенные диагностики. Для каждого наблюдения могут быть вычислены значения канонических переменных, которые затем можно просмотреть на встроенных пиктографиках (а также добавить к файлу данных).
В этом модуле реализован полный набор методов канонического анализа (дополняющий методы канонического анализа, встроенные в другие модули). Работать можно как с файлами исходных данных, так и с корреляционными матрицами; вычисляются все стандартные статистики канонической корреляции (собственные векторы и собственные значения, коэффициенты избыточности, канонические веса, нагрузки, дисперсии, критерии значимости для каждого из корней и др.), а также некоторые расширенные диагностики. Для каждого наблюдения могут быть вычислены значения канонических переменных, которые затем можно просмотреть на встроенных пиктографиках (а также добавить к файлу данных). 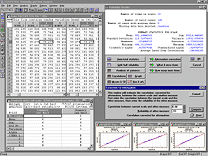 Этот модуль включает широкий набор процедур для разработки и оценки выборочных исследований и опросных листов. Как и во всех модулях системы
Этот модуль включает широкий набор процедур для разработки и оценки выборочных исследований и опросных листов. Как и во всех модулях системы 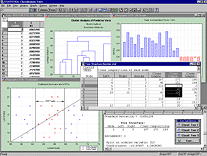 Модуль Деревья классификации системы
Модуль Деревья классификации системы 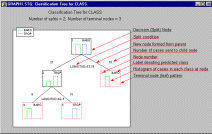 Пользователь может также задавать кратность кросс-проверки во время построения дерева и для оценки ошибки, параметр SE-правила, минимальное число объектов в вершине отсечения, начальное число для датчика случайных чисел и параметр альфа для отбора переменных. Исследовать входные и выходные данные помогают встроенные графические средства.
Пользователь может также задавать кратность кросс-проверки во время построения дерева и для оценки ошибки, параметр SE-правила, минимальное число объектов в вершине отсечения, начальное число для датчика случайных чисел и параметр альфа для отбора переменных. Исследовать входные и выходные данные помогают встроенные графические средства.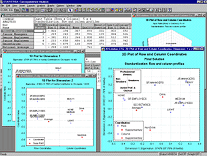 Этот модуль содержит полную реализацию методов простого и многомерного анализа соответствий, в нем можно анализировать таблицы очень больших размеров. Программа воспринимает следующие типы файлов данных: файлы, содержащие категоризованные переменные, по которым строится матрица сопряженности (кросс-классификации); файлы данных, содержащие частотные таблицы (или какие-либо другие меры соответствия, связи, сходства, неупорядоченности и т. д.) и кодовые переменные, определяющие (перечисляющие) ячейки входной таблицы; файлы данных, содержащие частоты (или другие меры соответствия). Например, пользователь может непосредственно создать и проанализировать частотную таблицу. Кроме того, в случае многомерного анализа соответствий имеется возможность в качестве входных данных непосредственно задать матрицу Берта.
Этот модуль содержит полную реализацию методов простого и многомерного анализа соответствий, в нем можно анализировать таблицы очень больших размеров. Программа воспринимает следующие типы файлов данных: файлы, содержащие категоризованные переменные, по которым строится матрица сопряженности (кросс-классификации); файлы данных, содержащие частотные таблицы (или какие-либо другие меры соответствия, связи, сходства, неупорядоченности и т. д.) и кодовые переменные, определяющие (перечисляющие) ячейки входной таблицы; файлы данных, содержащие частоты (или другие меры соответствия). Например, пользователь может непосредственно создать и проанализировать частотную таблицу. Кроме того, в случае многомерного анализа соответствий имеется возможность в качестве входных данных непосредственно задать матрицу Берта. 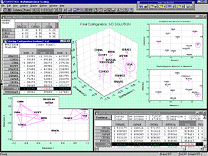 В модуле Многомерное шкалирование реализован полный набор методов (неметрического) многомерного шкалирования. Здесь можно анализировать матрицы сходства, различия и корреляций между переменными, а размерность пространства шкалирования может достигать 9. Начальная конфигурация может вычисляться программой (с помощью анализа главных компонент) или задаваться пользователем. Величина стресса и коэффициент отчуждения минимизируются с помощью специальной итерационной процедуры.
В модуле Многомерное шкалирование реализован полный набор методов (неметрического) многомерного шкалирования. Здесь можно анализировать матрицы сходства, различия и корреляций между переменными, а размерность пространства шкалирования может достигать 9. Начальная конфигурация может вычисляться программой (с помощью анализа главных компонент) или задаваться пользователем. Величина стресса и коэффициент отчуждения минимизируются с помощью специальной итерационной процедуры.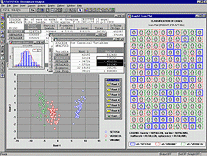 Модуль Дискриминантный анализ содержит полную реализацию методов пошагового дискриминантного анализа с помощью дискриминантных функций.
Модуль Дискриминантный анализ содержит полную реализацию методов пошагового дискриминантного анализа с помощью дискриминантных функций. 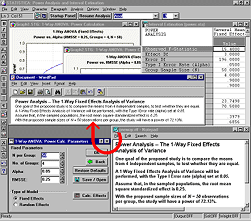 Используя модуль Анализ мощности STATISTICA при планировании и анализе данных, Вы можете всегда быть уверены в эффективности исследования. Очень печально, когда после длительного анализа оказывается, что выбранный вами метод не подходит из-за малого размера выборки.
Используя модуль Анализ мощности STATISTICA при планировании и анализе данных, Вы можете всегда быть уверены в эффективности исследования. Очень печально, когда после длительного анализа оказывается, что выбранный вами метод не подходит из-за малого размера выборки.